軟體開發中，資料結構就像是地基一樣，地基打得越穩，對我們再程式開發中絕對是百益而無害！(講講的🤣，其實是因為面試很常問，不得不學呀！）

本文會介紹普遍中計算機科學裡的資料結構有哪些😁

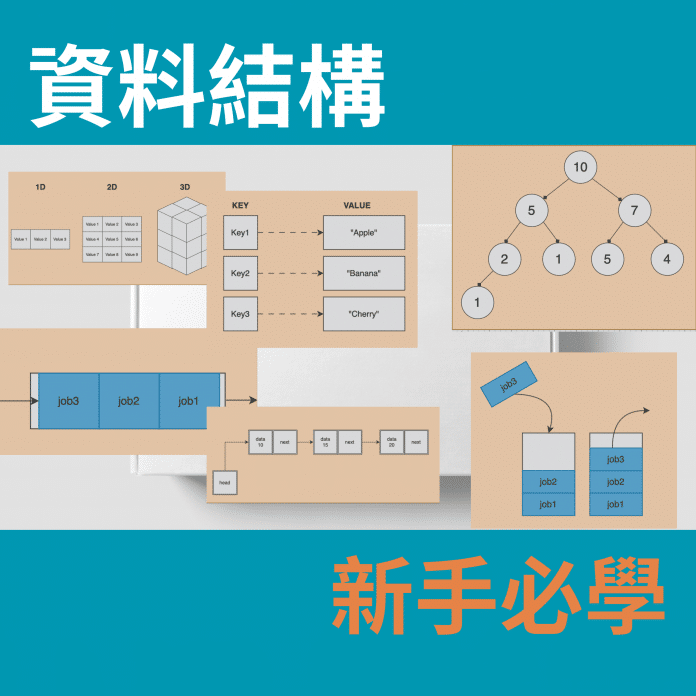
Array 陣列

• 用來儲存相同類型並擁有序列的記憶體空間
• 需事先宣告數據空間，因此有機率造成記憶體浪費
• 由於有序列，讀取和修改的速度很快
• 但要刪除和新增的速度會比較慢，因為陣列會需要重新排序
• Access: O(1)，因為你可以透過索引直接查找; Search: O(N)，需要完整遍歷, Insertion和Deletion: O(N)，刪除或新增後可能需要重新移動其他元素

比如Python裡的List以及Golang的Array，都屬於陣列的資料結構。

# Python
# 可以透過 my_array[0]來獲取數組
my_array = [1, 2, 3, 4]
my_array[0] = 10 # my_array=[10, 2, 3, 4]

######

# Go
// 可以透過 宣告 myArray來獲取固定長度的陣列
var myArray [5]int
// 也可以同時賦值
myArray := [5]int{1, 2, 3, 4} // 不足的地方預設為0 [1,2,3,4,0]
myArray[3] = 30 // [1, 2, 3, 30]

Linked Lists

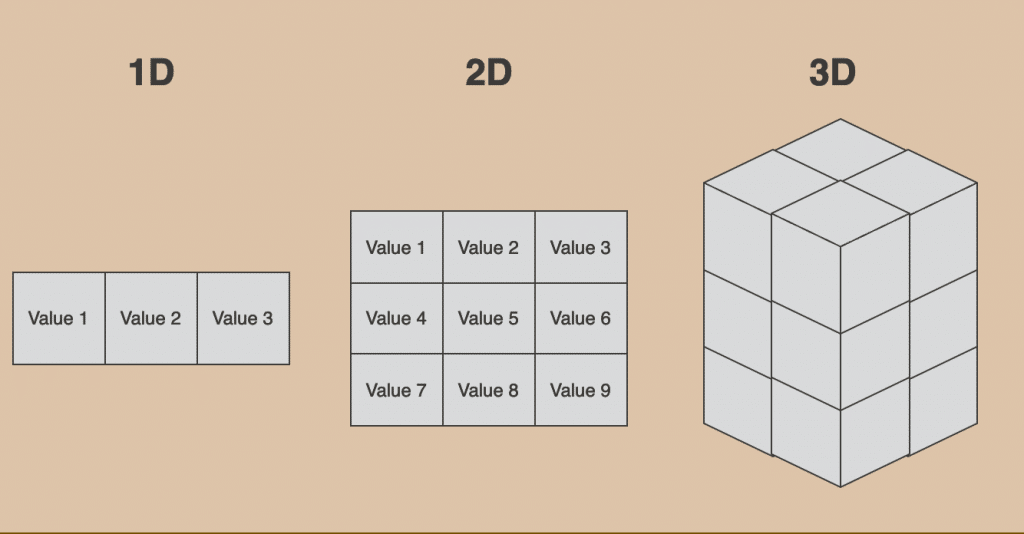
• 一個資料會指向到下一個資料
• 容量小，不需要事先定義一塊空間給它，資料包含一個指針指向下一個Linked list和數據值
• 當要讀取資料時，每次都必須要從頭開始遍歷一次，比Array慢
• 要插入或刪除資料時，只要把前一個的Node指向要替換的資料，並讓想替換的資料指向後一個（像火車接鐵軌那樣），速度比Array快

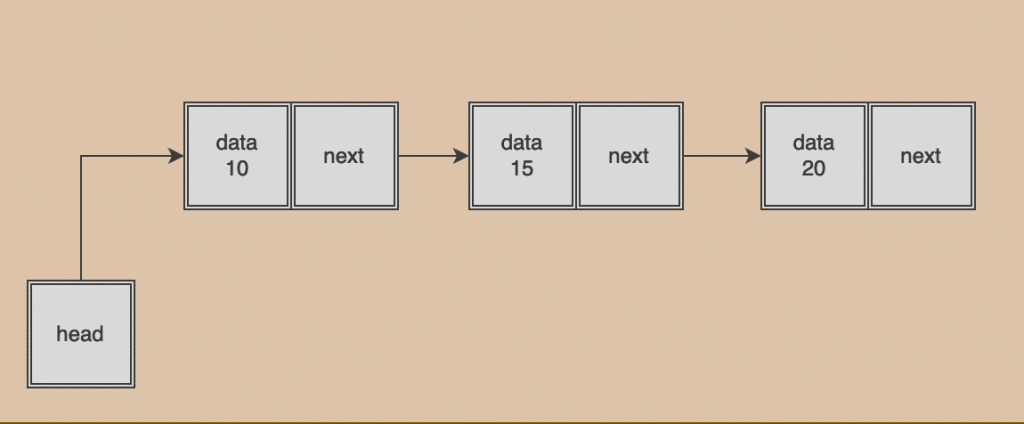
Hash Table 雜湊表

• 擁有Key和Value，一個Key會mapping到一個Value
• 之所以叫雜湊(hash)表，是因為他的索引(index)是透過Key經過Hash運算後得到，因此同樣的Key會產生衝突(因此有延伸出很多解決方案，但這裡就不展開了)，而索引的範圍從0~N-1
• 資料型別不受限制，比如你可以是 {"key": 123} or{321: "key"} 甚至 {-5: "blabla"}
• 時間複雜度為O(1)

Heaps

• 屬於完全的二元樹(Complete Binary Tree)
• 從上而下，從左而右，且父節點會永遠大於等於或是小於等於下方的兩個子節點，又稱為Min Heap或是Max Heap
• 自帶優先順序的排序，可應用於一些需要優先順序的任務
• Insert和Delete的時間複雜度為O(logN)、Heapify: O(N)、Peak: O(1)
• 建構的複雜度則是 O(N)

補充一下：Heapify的用意是為了重新排序整個Heaps

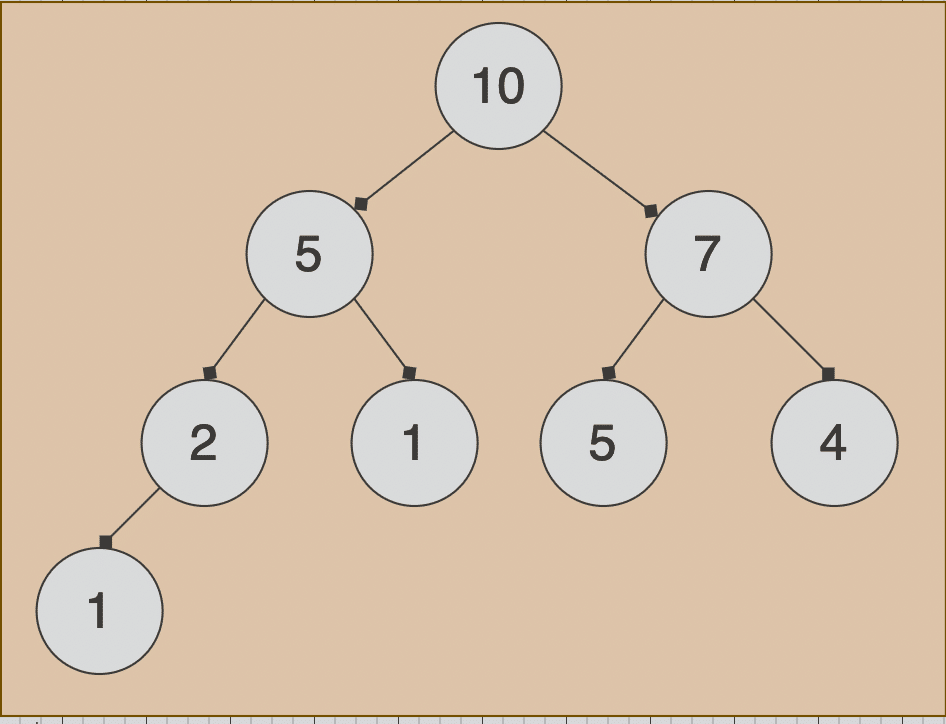
Python 裡面稱作堆，而Java裡稱作Priority Queue，實務上你可以使用Array來表示一個Heap，如下

Parent: ( n - 1 ) / 2

left child node: 2 * n + 1

right child node: 2 * n + 2

比如說，我們上圖Max Heap可用Array表示 [10, 5, 7, 2, 1, 5, 4, 1]，對節點5(index=1)來說，他的父節點等於( 1 - 1 ) / 2 = 0，也就是10

而子節點分別會是 2 * 1 + 1 = 3和 2 * 1 + 2 = 4，剛好對應到Array裡的2和1

舉個小案例：

比如說我們有一個Cluster管控多台Hypervisors，並且每台Hypervisor上都有多台VMs，當今天使用者想要刪除VM時，我們可以透過Heap的特性把Hypervisor和VM綁再一起並傳入Heap，再刪除時，Heap就可以直接給出最適合優先刪除VM的Hypervisor資訊，達到優先刪除減輕負擔的效果，同理也可以應用到新增VM。

Stack

• LIFO(Last In First Out)，先進去的任務會最後處理，就像放盤子一樣。
• pop 、push、 peak的時間複雜度都是 O(1)
• 可用Array或是Linked list來實作

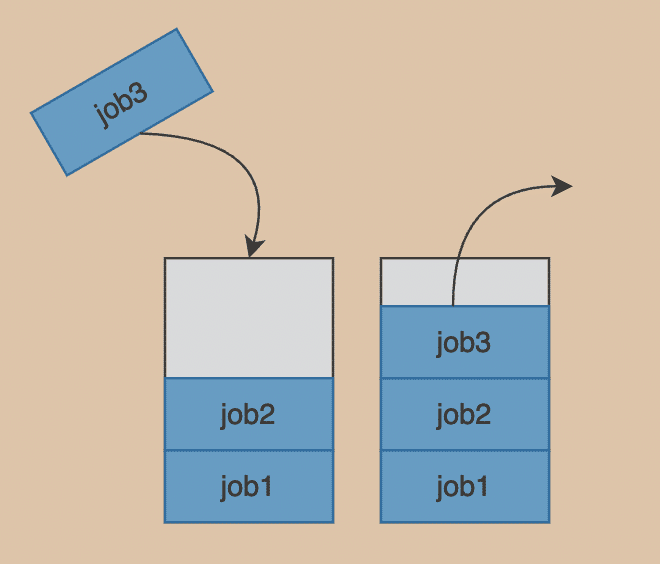
就像是寫程式時回上一步或是瀏覽器上一頁，其實就是Stack的概念

Queue

• FIFO, First In First Out 先進先出，就像排隊買票一樣～
• Enqueue表示插入Queue、Dequeue表示從Queue中抽出，Peak在下圖中表示獲取當前要即刻處理的job1
• Enqueue、 Dequeue、Peak的時間複雜度皆為O(1)
• Lookup 的時間複雜度為O(N)

非常直觀，簡單來說就是會照順序往下一直執行的結構。

Trees

除了上面提到的Heap是Tree的一種之外，常見的Tree還分別有

1. BFS(Breadth-First Search) 寬度優先搜索

• 目標 : 列出捷徑、最短距離、所有路徑
• 需要額外的記憶體來儲存待處理的節點

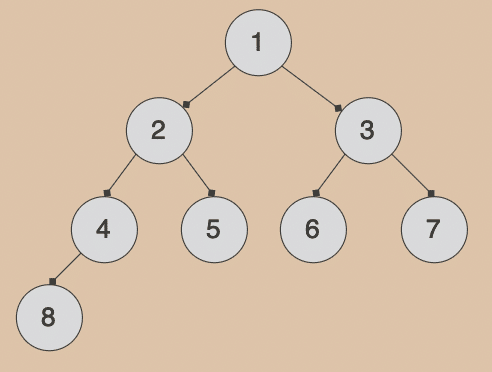
2. DFS(Depth-First Search) 深度優先搜索

• 直接一路到底，所以在某些時候會比廣度搜尋來得有效率
• 比較省記憶體，因為一次只需要維護一條路徑上的數據來進行搜尋

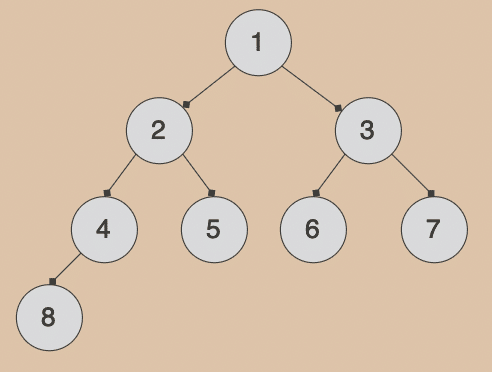
要是你有在刷題的話，應該會很常需要去考量數據的結構和執行邏輯，通常當你擁有清晰的資料結構邏輯，你就能夠清楚的知道該怎麼解題，通過以上對資料結構的圖解，相信能夠對你產生幫助！

那，我們下次見囉✌️～

有興趣的話也可以觀看我的上一篇文章唷：Context Manager是什麼

參考連結

樹(資料結構)